Instrumentation applications of ultra-precise Fast Fourier Transformation (FFT), powered by the Precise, Repeat Integral Signal Monitor (PRISM) algorithm
Applications: signal processing, spectral analysis, FFT, ultra-precise frequency, phase and amplitude measurement
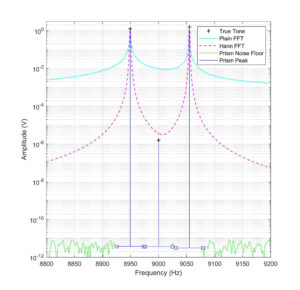
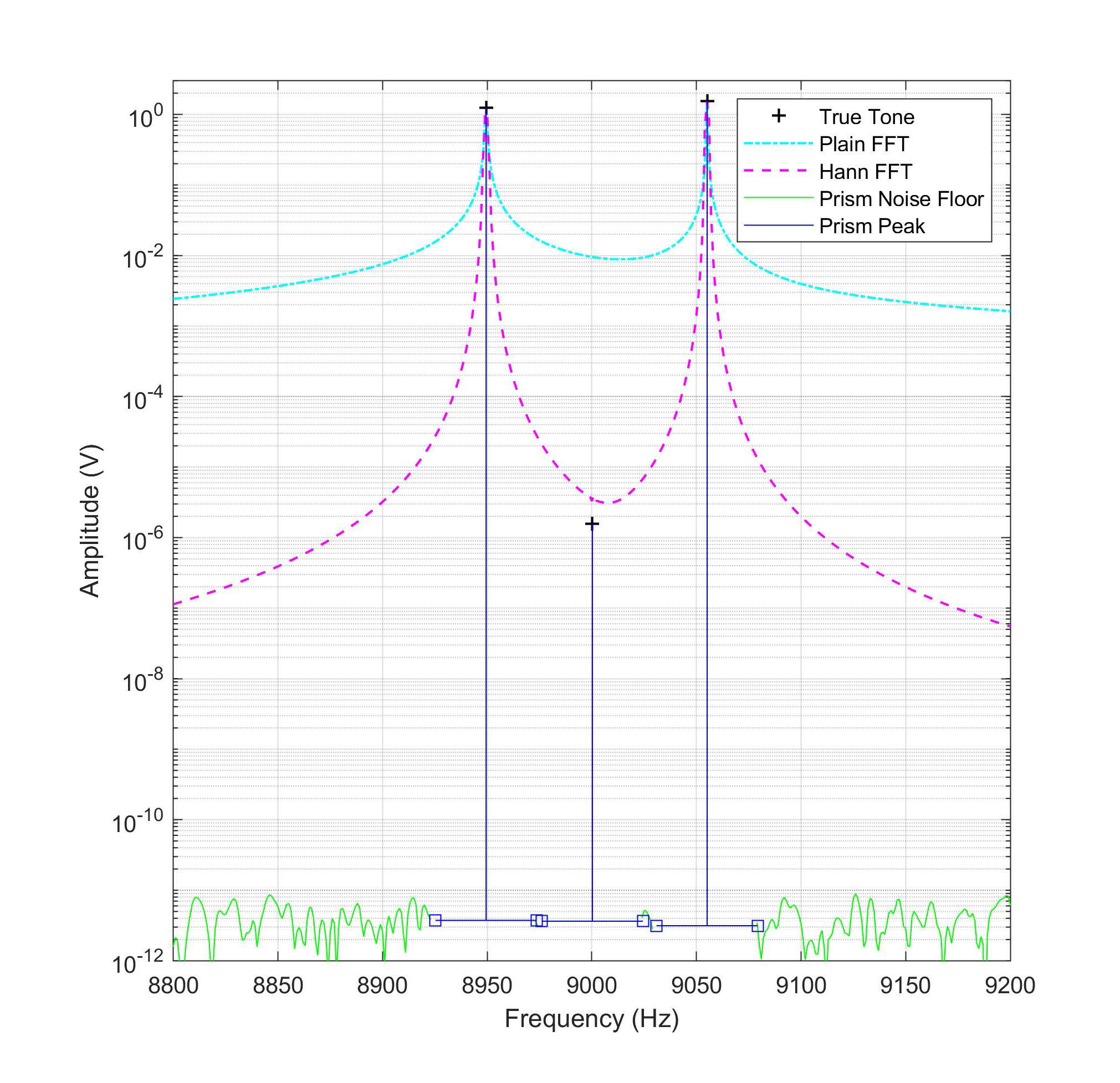
The prism FFT technique uses two windowing functions to calculate the exact tone frequency and amplitude.
In the example shown, the two outer tones are correctly calculated to 12 decimal places, while the middle tone is computed to 6 decimal places. These high precision results are achieved using only twice the computational cost of conventional FFT methods.
| Features | Benefits |
|---|---|
|
|
|
|
|
|
|
|
|
|
1: 106 improvement in frequency calculation compared to conventional Hanning approach
Patented & available for:
- Licensing
- Co-development
- Consulting
Learn more – enquiries@innovation.ox.ac.uk
Browse more opportunities – www.innovation.ox.ac.uk
about this technology
© Oxford University Innovation

